Las matemáticas de la cultura Andina se
desarrollaron de manera muy abstracta, subdividiéndose en diferentes áreas,
tuvieron grandes aportes y una manera muy peculiar de concebir el mundo.
Se ha mencionado que el desarrollo en la geometría fue muy
sobresaliente, en culturas tales como la egipcia, la babilónica y la china; sin
embargo ninguna de estas llego a tener una estructuración y sistematización axiomática
tan rigurosa como la tuvo la euclidiana, presentada al modo los elementos de
Euclides. Por su parte, las culturas
asentadas en la zona de los Andes demostraron grandes conocimientos en ésta área,
tanto a nivel cualitativo como cuantitativo, estas se dividieron en dos ramas:
La geometría analítica fractal, que es incomprensible hasta la actualidad y la
geometría Arborescente, que combinadas dieron lugar a el Kipu, el cual consistía
en un sistema de referencia por medio del cual se hacían predicciones, cuentas
y mediciones cualitativas; Es decir, concebían el mundo desde una cosmovisión geométrica.
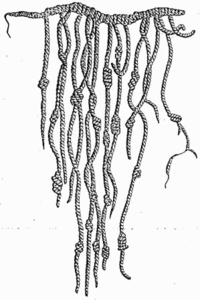 |
Ilustración 1 Kipu wolna
|
Utilizaron
un sistema de representación geométrica denominado “sistema de cruz cuadrada”
que se basaba en una distribución de cruces concéntricas, constituyendo un cuerpo
topológico fractal muy distinto al sistema cartesiano conocido en la
actualidad. En ese sistema podían estudiar las propiedades de funciones
discretas, más eficiente que el sistema de puntos que solamente describe los
movimientos de una partícula.
Sobre este sistema se hizo la construcción en
un ente geométrico simbólico llamado la “Chakana”, que tiene relación con la
agricultura, la distribución del agua y
las constelaciones.
 |
Ilustración 2 la Chakana
|
Las matemáticas
arborescentes van más relacionadas a la estructuración lógica del Kipu, es un
sistema de representación en el espacio con variaciones del métrico. El nuevo
espacio va en relación al entorno del hombre andino, proveniente de la
naturaleza, relacionado con su estructura
y su proceso reproductivo. En este sistema las combinaciones genéticas se podían
simular mediante nudos y ramas,
calculando así las características del descendiente y su parentesco.
Aunque el kipu originalmente fue creado para
la predicción por medio de experimentación agrícola a causa de las catástrofes climatológicas
y algunos fenómenos, su uso trascendió tanto en el uso agrícola, como en la
astronomía, astrología, historia, los
juicios y otros, teniendo en cuenta que este conlleva una gran dificultad deliberativa por el tipo,
color y distanciamiento de los nudos, con diferentes interpretaciones.
Por otro lado, es importante mencionar la
manera en que los andinos desarrollaron la aritmética con tanta eficiencia,
utilizando dos instrumentos llamados la “yupana” y la “tapana”, en los cuales emplearon
la notación de arriba hacia abajo, no por renglón seguido, forma en la que
contaban. Según la literatura en los últimos 500 años del reino Inca, se utilizó
una escritura imperfecta de archivos o depósitos, hechos en madera, piedra o
barro, con separaciones en las cuales introducían piedras de distintos tamaños,
colores y formas, brindando información de cuentas puntuales que realizaban
ciertos miembros.
 |
Ilustración 3yupana-trton
|
El siguiente video muestra la composición de la yupana, y algunas operaciones sencillas que se podían realizar con la misma.